Rymdhamster
ɹǝʇsɯɐɥpɯʎɹ
Hur menar du nu?Sedan avlutar han med ett antagande att ((X/(X+1)) * Y )+0,5 är den korrekta formeln för verkliga tärningar, vilket uppenbart inte är korrekt (det stämmer bara för X=1).
Hur menar du nu?Sedan avlutar han med ett antagande att ((X/(X+1)) * Y )+0,5 är den korrekta formeln för verkliga tärningar, vilket uppenbart inte är korrekt (det stämmer bara för X=1).
Säg att du spelar på stryktipset (slumpartade rader). Och så en dag säger du: Idag ska jag förbättra mina chanser, så jag spelar 10 olika rader istället för en rad. Säger du då attDet stämmer, men är ointressant.
"Din chans ökar med 100%"
"Sweet, då lyckas jag automatiskt!"
"Nejnejnej, jag menar 100% av vad du har nu, alltså en fördubbling."
"Men... jag har ju bara 5% i grund."
"Så grattis, nu har du 10% chans att lyckas!"
"
"
Om jag läser det du skriver så tolkar jag det som att en kompentent person med advantage får liten fördel, men en inkompentent person med disadvantage får stor nackdel... men det kanske inte är det du skrev.Att en expert får knappt någon fördel av advantage är väl vettigt, likadant att någon som knappt kan något har otrolig svårt om disadvantage. De ska ju inte ens slå ett slag i sådana fall.
Det tror jag också.Tror det bara är vanan av linjära system (BRP, d20) som spelar in.
Nej, vi pratar visst om olika saker här. Antagligen för att din post var inne på (åtminstone) två olika frågor.När du säger "ointressant", så menar du att att det är ointressant, för att det ändå inte komme inträffa.
Jag kompletterade ju min post med en "Edit". ((X/(X+1)) * Y )+0,5 är alltså gränsvärdet när antalet tärningssidor går mot oändligheten, För en tärning med ett begränsat antal sidor (dvs en verklig tärning) ligger värdet i närheten av detta gränsvärde, men det är inte exakt lika.Hur menar du nu?
Tyckte du att det var ohövligt? Då skulle du hört min lärare i Matematisk statistik, när någon gjorde på det viset.Jag är säker på att du kan uttrycka dig hövligare än så.
Det går att analysera sannolikheter och svårigheter i rollspel på flera sätt och det blir olika slutsatser om man jämför förändring av chans att lyckas eller risk att misslyckas.
Ah... ja, han sa ju att det mest var "tillräckligt nära" för att reflektera över de tärningsslag som är aktuella för att spela lite rollspel =)För en tärning med ett begränsat antal sidor (dvs en verklig tärning) ligger värdet i närheten av detta gränsvärde, men det är inte exakt lika.
Då måste jag fråga; varför har du denna förväntan? Mig veterligen står det inte någonstans i reglerna för D&D.det är ju där jag har den subjektiva förväntan att man har 1/20 att misslyckas oavsett hur bra man är, och att man har 1/20 att lyckas oavsett hur dålig man är. Och det är den förväntan Adv/Dis bryter mot, efterso det i praktiken blir så svårt att det är onödigt att slå (eller så lätt).
Men du fortsätter motsäga dig själv.Nej, vi pratar visst om olika saker här. Antagligen för att din post var inne på (åtminstone) två olika frågor.
Vad jag försökte göra var att förstärka Oldtimers poäng att relativa förändringar av sannolikhet inte är speciellt intressanta i spel. Det en spelare vill veta är "Hur många utfall lyckas med den här modifikationen, som annars skulle ha misslyckats?" Det är det enda man bryr sig om.
Sedan är ditt svar inne på poängen att chansen för fummel på en d20 nästan försvinner och chansen för en crit nästan fördubblas. Där ser du en bug. Jag ser en feature.
Vidare finns fenomenet att förändringen av sannolikhet blir störst om utgångsläget är att man ligger runt 50%, medan fördelarna blir mindre ju närmare man är ytterligheterna på skalan. Återigen ser jag detta som rätt snyggt, och har inga problem med att motivera det i fiktionen.
För att det fortfarande gör det meningsfullt att försöka, eller farligt att riskera något.Då måste jag fråga; varför har du denna förväntan? Mig veterligen står det inte någonstans i reglerna för D&D.
Hur då? Du fortsätter ju att prata om två olika saker. Tycker du att de motsäger varandra? För det gör de inte, de är bara olika.Men du fortsätter motsäga dig själv.
Båda är såklart intressanta att diskutera - om man förstår varför man använder den varianten man använder.Den första frågan handlar om ifall det är intressant att diskutera relativa eller absoluta skillnader.
Och som jag då visade ovan så har det få fördelar och flera nackelar, att tolka Advantage som "slå två tärningar" jämfört med att tolka Advantage som "du får +5, men misslyckas fortfarande om du slår etta.Den andra frågan handlar om transparens/intuitivitet kontra snabbhet/spelbarhet.
Jo, men man kan inte låtsas som att bara absoluta skillnader är väsentliga. Eller att de är bättre eller mer korrekta. Eller att vår vardagliga intuition eller vårt vardagliga språk förutsätter absoluta skillnader över relativa skillnader.Man kan ha vilken kombination som helst av åsikter om dessa två frågor utan att de motsäger varandra.
Vi får väl "agree to disagree".Och som jag då visade ovan så har det få fördelar och flera nackelar, att tolka Advantage som "slå två tärningar" jämfört med att tolka Advantage som "du får +5, men misslyckas fortfarande om du slår etta.
Dito.Jo, men man kan inte låtsas som att bara absoluta skillnader är väsentliga. Eller att de är bättre eller mer korrekta. Eller att vår vardagliga intuition eller vårt vardagliga språk förutsätter absoluta skillnader över relativa skillnader.
Okej, så det är bara en personlig uppfattning som kommer av att spel baserat på t20 historiskt inte kunde ha mindre enheter än 1/20.För att det fortfarande gör det meningsfullt att försöka, eller farligt att riskera något.
Jag skulle säga att 1/20 är ganska "lagom" för minsta chans att lyckas, eller minsta chans att misslyckas.
Well, det var ju 1/20 också i T100-baserade spel, som jag skrev.Okej, så det är bara en personlig uppfattning som kommer av att spel baserat på t20 historiskt inte kunde ha mindre enheter än 1/20.
Men om du är så dålig att du behöver 20 för att träffa ett mål mitt på dagen och det nu är mörkt och du bara skymtar målet, så känner ju jag att din möjlighet att träffa bör vara försvinnande liten. Typ 1/400. Det är ganska "lagom" för mig.
Det är väl deras rimlighet vi diskuterar här? Och jag är övertygad om att deras syfte också är att vara rimliga."lagom": givet att Advantages inte ackumuleras så ser jag ingen anledning att diskutera deras rimlighet/realism. Det är inte deras syftet. Syftet är att det ska vara snabbt, enkelt och roligt, och är det väsentligen.
Det tror jag inte alls.Det är väl deras rimlighet vi diskuterar här? Och jag är övertygad om att deras syfte också är att vara rimliga.
Ah, du tänkte på den grejen. Ja, där håller jag med dig helt. Det är en rejäl bugg enligt min enkla åsikt. De borde ackumulera.Det tror jag inte alls.
Advantage-system kan varken vara rimligt eller realistiskt, eftersom det inte accumulerar effekter.
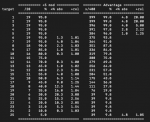
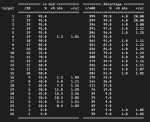
Och som min data visar... så länge man rör sig mellan 20-80% chans att lyckas, så är skilladen ovästenlig (på +5 eller Advantage).Ah, du tänkte på den grejen. Ja, där håller jag med dig helt. Det är en rejäl bugg enligt min enkla åsikt. De borde ackumulera.
Jag kan ju nämna att jag gjorde ett spelsystem som helt bygger på t20 med ackumulerande advantage/disadvantage och använde i mitt Cthulhu: Preludium. Fungerar utmärkt.
Den stora skillnaden på +X och Advantage är ju att +X gör det möjligt att klara svårare utmaningar. Nu kör ju inte jag (eller D&D) med att man alltid lyckas på 20 och misslyckas på 1 när det gäller färdigheter, så +X höjer alltså din faktiska förmåga, medan Advantage bara ger dig högre sannolikhet att lyckas med sådant du redan kan lyckas med.Och som min data visar... så länge man rör sig mellan 20-80% chans att lyckas, så är skilladen ovästenlig (på +5 eller Advantage).
Och då skulle jag GISSA att +8 ganska väl motsvarar dubbel-advantage (men kanske bara om man har 50-80% från början).
Problemet är svansarna. Där det blir extremt förutsägbart med multipla Advantage/Disadvantage, jämfört med att man alltid lyckas på 20 och misslyckas på 1, oavsett hur mycket plus/minus man har.
