Kranks arbetsdagbok

[krank]

UPPDATERING 2021-02-22

• Rotsystem: Alla kungens hästar… – Fyra sidor. Yay! En av dem har en karta på sig. Jag noterar att det trots allt blir någon form av bild på ganska många av de här sidorna. Nice. Sista sidan är just nu 143, och det här delävantyret är på 56 sidor.

 

[krank]

UPPDATERING 2021-02-26

• Rotsystem: Alla kungens hästar… – "Hit man kommer när man kommer hem" har nu en komplett grovlayout där alla bilder och tabeller ligger där de ska. Det betyder att det bara är ett äventyr kvar, sedan är alla tre redo för nästa vända – då jag letar onödiga avstavningar och sånt. Och fixar kolofonen på riktigt. Därefter väntar arbetet med sidhänvisningar och, såklart, registret och innehållsförteckningen. Äventyret landade på 62 layoutade sidor, och modulen är nu totalt 149 sidor lång.
• Kutulu: Mardrömmar från Amerikat – Det har inte hänt så mycket den här veckan, och det är mestadels mitt fel tror jag. Jag behöver fixa fram en mall till kontrakt till vår omslagsillustratör. Jag är ju i vanliga fall ganska oproffsig här och kör på rena muntliga överenskommelser, men den här illustratören vill (fullt rimligt) ha kontrakt och då ska jag väl kunna fixa det. Jag tror jag dragit i rätt trådar och kommer förhoppningsvis ha ett kontrakt snart. Annars ska jag väl mest göra ett par handouts, framför allt en karta över en zeppelinare…
• Mothership: Gradient Descent – Ett sätt jag brukar hantera stress på är att skapa nya projekt. Det verkar kanske lite kontraintuitivt att jag skaffar mig mer att göra för att hantera att jag har mycket att göra, men hear me out: Jag skapar nya projekt där ingen förväntar sig något av mig. Alltså, projekt jag kan försjunka i kravlöst och utan deadlines. Sedan riskerar ofta de projekten att svälla till något som ska ges ut och har en deadline likförbannat, men åtminstone i början går det ju bra. Och ett säkert sätt att se till så projekt inte kommer att kunna bli "riktiga" är ju att förbereda saker till spel som ägs av nån annan, där allt material jag hanterar är upphovsrättsskyddat. Jag kommer inte att kunna ge ut det. Så jag har börjat skapa lite egna play aids inför en hypotetisk Gradient Descent-kampanj.
• Ödesväktarna: Fenix-äventyret – Slutversionen av illustrationen har levererats. Jag ska försöka styra upp betalning på söndag, då jag har möte med mina medförfattare. Jag ska också gå igenom korren under helgen; jag har fått in åtminstone några kommentarer. Jag antar att resten är OK =)

Puh, det tror jag var allt just för tillfället…

 

[Vimes]

"Midnatt"

När kommer det!?

 

[krank]

När kommer det!?

Rymd-Ödesväktarna? Tidigast 2023, skulle jag tro.

 

[krank]

UPPDATERING 2021-02-27

• Volt – Jag tog äntligen tag i att skriva in regeln kring att avvakta i strid, och det tror jag betyder att texten är "klar". Jag inväntar bekräftelse, men sen finns det risk att jag börjar layouta. Kanske redan i veckan.
• Ödesväktarna: Fenix-äventyret – Jag har gått igenom den lilla korr som kommit in, samt lagt till ett par meningar om att vävargillet inte gillar välgörenhet. Texten är i princip redo att skickas in; jag fixar det i morgon.
• More than Human – Några grejer föll på plats i mitt huvud och jag började skriva på ett slags översikt-dokument med teman jag vill fokusera på i More than Human version två, och lite hur jag pusslar ihop metaplotten och kampanjhemligheterna. Det blir inte riktigt som i version ett.

Jag tror att det var allt för idag.

 

[krank]

UPPDATERING 2021-02-28

• Ödesväktarna: Fenix-äventyret – Jag lade allra sista handen vid texten och mailade iväg det hela till Fenixredaktionen. Vi hade också vårt vanliga söndagsmöte, där vi bestämde att vi denna gång skulle dela lika på kostnaden för illustrationen. Jag skickade summan till Ronja, så tar mina kumpaner och swishar mig sen. Nu är iaf fenix-äventyret färdigt och klart och över. Det är ganska skönt att bli klar med grejer också.
• Ödesväktarna: Rymd – Förr eller senare kommer vi att behöva ett bättre namn på det här. Tyvärr målade vi ju in oss lite i ett hörn när vi döpte första spelet till Ödesväktarna – i det här andra spelet i samma värld (fast långt senare) så spelar man ju inte ödesväktare längre… Men idag tog vi i varje fall ett snack om metaplot och historia, och hur vi knyter samman de båda spelen på ett sätt som känns tillfredsställande för folk som spelat Ödesväktarna. Vad som hände med Vävargillet och med Urkrafterna och demonerna och drakarna, som vi faktiskt borde skriva något om och sluta hålla så himla hemliga. Jag får se till så mitt nästa äventyr har med en drake, helt enkelt.
• Mothership – Jag upptäckte att det fanns en vapentabell, och att det i den fanns en massa info jag inte hade med på mina vapenkort. Och tyvärr håller de på och krånglar med distansmått i meter… Jag som var glad över att Mothership förenklat saker och ting och bara körde med abstrakta short/medium/long. Så nä, de kör med olika distanser för olika vapen… Blergh. Jag är rätt sugen på att husregla det här, men tills jag gör det har jag iaf skrivit av vapentabellen in i Google Sheets. Jag är också i princip klar med min regelsammanfattning, så nu ska jag bara layouta alltsammans.

 

[krank]

UPPDATERING 2021-03-03

• Volt – Jag har gjort layout av de två kapitel vi har. Det som är kvar där är lite sidhänvisningar, ett register, och ett appendix med tabeller och regelsammanfattningar. Totalt klockar vi just nu in på 34 sidor, jag blir inte förvånad om vi landar i 40 innan vi är klara. Det är egentligen ett ganska litet system, men med luftig layout och en del bilder blir det ändå sidor av det, så att säga.
• Kutulu: Mardrömmar från Amerikat – Alla porträtt är levererade och 50% av stämningsbilderna. Jag är just nu mitt uppe i att försöka lösa vad vi kan kalla "de tråkiga bitarna", alltså ekonomin och sådant. Vi är ganska nära ett fungerande kontrakt med Regin Wellander, som gör omslaget.

När jag räknar ihop alla utgifter för projektet landar jag på 49 250:-. Det blir, inser jag nu, nog det absolut dyraste projekt jag givit mig in på. More than Human kostade, exkl tryckkostnad, på c:a 21 000:- och Rotsystem låg på c:a 19 000:-. Mycket av skillnaden handlar om att jag dels skrev de böckerna själv, och dels att jag denna gång har en omslagsillustratör som tar skäligt betalt.

Totalt är sveriges rollspelsförlag skyldiga mig lite över 37 000:-, men det är svårt att dela upp fakturorna så att jag utnyttjar hela den summan; med lite pusslande tror jag att jag kommer att kunna betala totalt 35 500:- den vägen. Resten, alltså 13.7k, kommer jag som det ser ut just nu att få ta ur egen ficka, om jag inte hittar något annat sätt att lösa det.

Jag vill vara tydlig med att det här alltså inte är jag som beklagar mig, utan bara jag som är transparent. Det är såhär mitt rollspelsmakande ser ut; ekonomiskt har det alltid varit en katastrof om målet varit att "gå runt".

 

[krank]

UPPDATERING 2021-03-04

• Rotsystem: Alla kungens hästar… – Jag har börjat layouta bokens sista äventyr, "Ambassadören som försvann". Äventyrets brödtext är inplacerad, så nu går jag igenom och försöker justera texten så den får plats snyggt samt stoppar in illustrationer, placeholders och SLP-profiler. Jag har också börjat göra en lista med illustrationer jag behöver göra – kartor, loggor och sånt. Slutligen har jag börjat skissa på loggorna till de olika organisationerna, och loggan till Theseusorden har fått mig att börja lära mig hur man gör retopologisering i Blender – jag sitter just nu och gör om en fin högupplöst 3D-modell till en betydligt mer low poly dylik, just för att den ska vara med som en del av en logga. Mer jobb än det är värt? Visst, men det är ganska trevligt.
• Volt – Skapat dokument för appendix. Vapen- och rustningslistorna ska fyllas på av mina medskapare, och innan det är gjort så ligger nog det här arbetet en smula på is.
• Kutulu: Mardrömmar från Amerikat – Kontraktet med Regin är typ klart, ska bara skriva under och fixa. Det ekonomiska… Well. Det löser sig nog. Jag känner mig lite mindre nervös än jag gjorde igår.

Jag funderar på att eventuellt börja layouta engelska Ödesväktarna i morgon. Där är ju också ett projekt som egentligen är typ klart; jag har ju allt jag behöver egentligen. Och det vore najs att få undan ett projekt.

 

[krank]

UPPDATERING 2021-03-05

• Kutulu: Mardrömmar från Amerikat – Kontraktet skickat till Regin. Jag borde sätta mig och göra en zeppelinarkarta i morgon, nu när jag börjar bli mer varm i kläderna i Affinity Designer. Men just idag hände det inte så mycket mer med det här projektet.
• Rotsystem: Alla kungens hästar, alla kungens män – Jag har gjort en illustration! Eller kanske två. Also: layout.

Det tredje äventyret i "Alla kungens hästar…", Ambassadören som försvann, har hittills krympt med 524 ord genom att jag krånglat, fipplat och formulerat om för att få texten att passa in i min layoutmall. Mina korrläsare kanske blir lite förvånade sen när de läser slutprodukten, men sånt är livet. Om jag lagt in några nya fel är de felen i så fall 100% mina.

Just nu är äventyret 60 layoutade sidor långt och hela InDesign-boken 209 sidor. Det blir nog mer, skulle jag tro – åtminstone en 3–4 sidor till i det här äventyret (kartor…) och sen blir det ju efterspel och appendix. Jag är just nu på sida… typ 52 eller så i den här layoutvändan. Alla SLP:er är nu inlagda, och alla större bilder fram till just s 52. Nästa steg sedan blir att stoppa in alla SLP-porträtt.

Jag kom också på att jag… glömt två stora bilder som jag hade, så jag fick bråka lite både i föregående äventyr och det här för att få in dem. Men nu är det löst…

Jag gjorde också min egen första illustration på ett tag – den tidigare nämnda logotypen till Theseusorden. Nedan: En gråskale-version för användning på skärmar och i stor skala, och en monokrom för mindre skala. Jag blev ganska nöjd ändå, även om det tog ett par timmar att få till den fina low poly-looken. Och nu vet jag hur man retopologiserar i Blender =).

 

[krank]

UPPDATERING 2021-03-06

• Kutulu: Mardrömmar från Amerikat – Jag har reproducerat en ritning över en zeppelinare, som vi ska ha med i äventyret Terror på 200 meter.
• Rotsystem: Alla kungens hästar, alla kungens män – Jag har skapat en ny logga; den här betydligt tråkigare än Theseusloggan. Men en del loggor är ju helt enkelt lite tråkiga. Jag har också börjat skissa på en av de två återstående logotyperna som behövs till boken. Sen blir det ju dags för kartor…

Så, det här är zeppelinaren just nu:


Eventuellt justerar jag vissa linjers tjocklek och sånt framöver, vi får se.

Och det här är loggan:


Likheter med andra fiktiva företag med samma namn och liknande logga är fullt medvetna.

 

[krank]

UPPDATERING 2021-03-07

• Rotsystem: Alla kungens hästar, alla kungens män – Ännu en logga klar. Bara en kvar!
• Ödesväktarna RYMD – 100% arbetsnamn, men vi hade möte idag och styrde upp en hel del. Vi vet hur hur metagrejerna från Ödesväktarna med Ödesväven och Urkrafterna hänger ihop med Rymd-settingen, vi vet vilka rollpersonerna generellt är och vi vet vad vi behöver styra upp för att kunna speltesta lite. Sedan tidigare har vi också en grundstruktur för uppdrag. Det rör på sig, märkligt nog.
• Sentinels of the Weave – 40 sidor layoutade. En hel del omformulering och kapning fick göras i texten för att den skulle få plats, och vi har ändå en del sidor där texten tar slut innan sidan gör det – eftersom jag annars skulle behöva ha typ en rubrik och två rader text längst ner på en sida. Lite retsamt! Kapitlet om Elemin blev två sidor längre än i den svenska boken, men det i sig är ju inget problem.

Här är loggan jag gjorde idag:



Jag är nog helt OK med den; den är inte den logga jag gjort som jag är mest nöjd med men den är heller inte skitdålig. Men jag kan ju återkomma till den om jag kommer på något smart sätt att göra den bättre.

 

[krank]

UPPDATERING 2021-03-08

Första jobbdagen efter lovet… Så idag blev det mest jobb. Men lite hann jag med.

• Rotsystem: Alla kungens hästar, alla kungens män – Vertikal variant av Cortical-loggan & ett par sidor layout.

Ja, jag behövde en lite mer vertikal version att ha i ytterkanten på en boksida, så jag gjorde den här lite snabbt:



Nästan så att jag blev mer nöjd med den än med den horisontella…

Oh well.

Innan jag går vidare med layouten nu så måste jag nog göra ett par kartor, för jag vet inte alls hur mycket plats just de här kartorna kan tänkas ta. Som allra minst behöver jag skissa lite. Så: lite layoutpaus! I det projektet åtminstone. Jag har ju Sentinels of the Weave också. Dessutom borde jag nog egentligen börja med layouten av Mardrömmar från Amerikat snart också…

 

[krank]

UPPDATERING 2021-03-09

Allmänna motgångar åt upp en hel del av dagens energi, men jag lyckades iaf lägga typ 20 minuter på lite layoutande.

• Sentinels of the Weave – Lade till kapitel 2, det med organisationerna. 30 sidor i original, ser ut som 32 nu. Grovlayout gjord; alla bilder är typ där de ska och all text är lagd. Tog mig igenom sex sidor av textfippel också, för att få texten att passa bättre etc. Har identifierat några sidor i kapitlet som kommer att behöva lite extra sådan kärlek.

Jag har också fått en del bra respons på Cortical Systematics-loggan från olika håll. När jag samlat på mig lite energi så funderar jag på att göra något åt den.

 

[krank]

UPPDATERING 2021-03-10

• Sentinels of the Weave – Resten av kapitel 2 är genomgånget. 32 sidor. Inledande textfippel klart; allt får plats där jag vill ha det. Givetvis kommer jag att gå in och finjustera senare; det här är bara en grovis. Totalt har jag nu grovat klart 72 sidor; originalboken klockade in på 194 sidor så min gissning just nu är att vi landar på jämna 200 för den engelska versionen.
• Rotsystem: Alla kungens hästar, alla kungens män – Jag hittade funktionen "running header" i InDesign och gav mig såklart omedelbart i kast med att använda den.

I korthet är det alltså en placeholder man placerar i sin master page-mall och som ersätts med "senaste texten som sattes i stilmall X". I mitt fall valde jag stilmallen "Rubrik 1", så uppe i vänstra hörnet på varje sida finns nu den senaste nivå 1-rubriktexten. Det ger lite mer finkornig navigationshjälp än bara de rena kapitelnamnen.

Jag stötte dock på en märklig bugg på ett ställe, där jag inte fick det att funka – oavsett vad jag gjorde så struntade den helt i rubriken "Den andra expeditionen". Jag får försöka hitta en workaround sen. Eller så struntar jag bara i det.

I Alla kungens hästar upptäckte jag också ett ställe där jag stoppat in en illustration utan att ha fått undan all text som den ersatte. Så jag kommer att behöva gå in och trolla bort typ 8–10 rader lite senare. Men inte idag.

 

[krank]

UPPDATERING 2021-03-12

• Kutulu: Mardrömmar från Amerikat – Tittat på och godkänt kompositionsförslag för omslaget, och vidarebefordrat uppgifter illustratören behöver för att kunna fakturera rätt företag.
• Sentinels of the Weave – Kapitel 3 sparkar min rumpa. Det är bara 10 sidor i den svenska versionen, men den engelska är 11 – och 11 är ett dåligt tal, för jag har ingen ytterligare text och ingen ytterligare illustration att fylla ut den där tomma sidan med. Nästa kapitel ska ju börja på en högersida, precis som alla kapitel. Så… Just nu sitter jag och verkligen tok-bantar texter. Jag försöker undvika att ta bort information som finns i den svenska och bara plocka bort sånt jag lagt till under översättningen, och gör också en hel del omformuleringar. Det går långsamt! Jag är på typ sida 4 eller så.
• Mothership – Idag gjorde jag en mall för vapen. Det är en fin balans mellan lättlästhet och snygghet; jag är ännu inte riktigt nöjd. Antagligen gör jag texten lite mindre igen; nu blev den läsbar men inte så snygg.
• Rotsystem: Alla kungens hästar, alla kungens män – Egentligen inget riktigt relaterat till äventyret utom att konstatera att det är dags att göra isometriska kartor igen.

Jag har däremot undersökt Affinity Designer och konstaterat att avsaknaden av riktiga macros/actions gör att det nog inte känns som att jag kommer att börja göra kartor där ännu. Tyvärr, för annars har ju programmet finfina isometriska rutnät som jag är lite sugen på. Men bristen på actions, vettiga styles och fri transformering (inkl perspektiv) för att jag nog kör Illustrator den här gången också.

Så istället tog jag och fixade en refresher om hur jag brukar jobba – bland annat räknade jag om all matte och gjorde faktiska anteckningar den här gången, så att jag förhoppningsvis minns hur jag tänkt nästa gång. Nästa grej här blir att återskapa matten för skuggningen av cylinderformade objekt.

Lite visuella resultat från dagen:

Vapenmall till Mothership

Spoiler

Isometriska anteckningar

Spoiler

(Vid närmare eftertanke borde det nog bli 100% skugga tidigare? 1-2 steg kanske?)

 

[krank]

UPPDATERING 2021-03-13

Idag gick all min produktiva energi åt till jobb, men jag vaknade i varje fall och kom ihåg hur den sista delen av min isometri-matte hängde ihop.

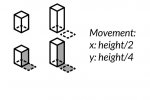
Alltså, stegen man gör när man vill förvandla en rak kvadrat till en isometrisk platta är alltså följande:

• Minska höjden till 80%
• Använder Shear-funktionen med gradtalet man får om man räknar ut arctan(2) minus arctan(0.5). Skälet till att det är just arctan(2) och arctan(0.5) är för att det är skillnaden mellan vinkeln som är just nu och vinkeln som vi vill ha. Arctan(2) är det för att vi har arctan(2/1)… Det har med proportionerna mellan bredden och höjden på de isometriska plattorna, okej? Jag kan inte förklara det här utan bilder.
• Och så roterar vi hela grejen moturs arctan(0.5) grader, så får vi den fina isometriska effekten där den romb vi byggt ställs på ett av sina hörn sådär snyggt.
• Resten är cleanup.

Men varför 80%? Det fanns i mina gamla illustrator-actions men jag kunde inte minnas hur fasen jag kom fram till det.

Men i morse vaknade jag och visste hur. Varning: matte. Dessutom från nån som egentligen inte kan matte. Eller ja, ligger nånstans mellan de som är riktigt dåliga på och avskyr matte, och de som kan matte på riktigt. Jag var estet på gymnasiet, liksom.


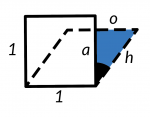
Det vi vill är ju att h efter att vi shearat ska vara lika lång som en av sidorna på ursprungs-kvadraten. För botten-kanten har ju inte ändrats, och ska det vara isometriskt så ska alla kanter vara lika långa. Men om vi bara shear:ar blir h för lång, för shear påverkar inte höjden.

Så det vi vill ha är förhållandet mellan 1 (originalhöjd) och a (målhöjd). 1 känner vi till. Hur räknar vi ut a?
Jo alltså, vi plockar fram gamla socka-toa. Eller ja, SOH CAH TOA (ja, jag har lärt ut trigonometri till elever genom att be dem föreställa sig strumpor i toaletter).
Vi har inte o, så varken SOH eller TOA är relevanta, de går inte att använda.

CAH är alltså cos(x) = a / h där x är vinkeln, a är sidan som är precis vid vinkeln (o är den på motsatt sida), och h är hypotenusan.

Och om cos(x) = a / h så är ju cos(x) × h = a. Och h – som är den önskade längden på den snedställda kanten – är ju 1. Och multiplicera med ett är ju ingenting.

Så allt vi behöver är egentligen cos(x) – det är allt. Och x vet vi vad det är – det är ju så mycket vi shearar med: arctan(2) - arctan(0.5).

Så formeln för att räkna ut a blir:

a = cos(arctan(2) - arctan(0.5))

Och stoppar man in "cos(arctan(2) - arctan(0.5))" i google så säger Google, hjälpsamt: 0.8.

Så om sidan är 1 och a är 0.8 så ska vi alltså minska höjden med 80%.


Låt ingen påstå att trigonometri inte är användbart utanför klassrummet! Mitt vanliga exempel brukar vara datorspel, där det ju generellt är väldigt användbart även om man inte ska göra speciellt matematiskt avancerade grejer. Men uppenbarligen är det också väldigt användbart när man gör isometriska rollspelsillustrationer =)

Det är också sånt här jag vill kunna göra till actions eller macros. Vilket är anledningen till att Affinity Designer inte riktigt är redo att hjälpa mig ännu.

En vacker dag ska jag hitta det vektorillustrations-program jag drömmer om. Det som är som ett parametriskt CAD-program när det gäller att skapa former och relationer mellan olika former, men som är som CSS eller något liknande när det gäller att definiera hur saker ska se ut. Det känns som att det borde kunna finnas…

 

[krank]

UPPDATERING 2021-03-14

• Ödesväktarna RYMD – Det här blir kanske den mest nischade produkt jag haft nöjet att göra något av, men mina medskapare är engagerade och det är alltid roligt att göra saker med folk som brinner för saker =) Idag hade vi möte, som vanligt.

Alltså, jag tycker också att Ödesväktarna RYMD (arbetsnamn) är ett roligt projekt och jag har haft roligt när jag varit spelare även i scifi-versionen av det här gamla fantasyspelet vi spelat i 20 år. Men jag kan inte undkomma en känsla av att det är ganska mycket inside baseball.

Anyways, konceptet just nu är i princip att rollpersonerna är två intressanta saker samtidigt: 1) de är "utforskar/undersökar-team" ombord på ett större rymdskepp. Det är ett stort skepp, som åker runt och… gör grejer åt sina ägare. Rollpersonerna är ett "away team" av mercs (typ) som hänger på, får uppdrag, droppas av, gör uppdrag, hämtas upp. Uppdragen är av varierande sort, sådär som det brukar vara i traddspel, men ofta är det utforskning eller heists av olika slag som gäller. Lite mysterielösande, också. Jag tror att det blir lite mer stridigt än Ödesväktarna är, men det måste nog inte bli det.

Det andra rollpersonerna är, är tjänare åt Urkrafterna, som försöker hålla sig undan från Ödesväktare som jagar dem. De har krafter, och en kontakt i form av en demon eller liknande som ger dem instruktioner. Så: en liten twist. Ombytta roller, kanske man kan säga.

Så det blir inte bara en reskin av Traveller.

Sen pratade vi lite om teknologinivån (extremt ojämn, man har avancerade datorer men använder dem bara där man absolut måste t.ex. vikrymdsdrift, men eftersom man hade en AI-relaterad kataklysm för ett tag sedan är man paranoid) och om hur folk anpassats för att kunna leva på olika planeter.

På det hela taget tror jag absolut att blir ett kul spel.

 

[krank]

UPPDATERING 2021-03-20

• Sentinels of the Weave – Kartan översatt liksom rollformuläret. Ungefär 50% av boken har fått en ruff layout. Jag siktar på att göra lite i morgon också.
• Universums Öde: Andromeda – Jag har dragit igång hjärnan och kopplat på den på det här projektet, så nu börjar den spotta ur sig idéer och spontanskapa strukturer. Jag har också köpt två böcker till av Johansson, som tekniskt sett inte utspelar sig i UÖ-universat men som jag ändå ska se om man kan låta sig inspireras av.
• Kutulu: Mardrömmar från Amerikat – Ekonomin verkar lösa sig, alla utom en inlage-bild är levererad, och jag har just gett tumme upp för en långt gången variant av det som ska bli omslaget.

Jag tror att jag pusslat ihop det ekonomiska nu, bland annat genom att Inhamnarna är så schyssta. Jag vet inte om jag nämnt det, men kostnaderna för illustrationerna och allt annat landade totalt sett en bit över vad jag har i skulder från olika rollspelsföretag, så jag kommer helt enkelt att på klassiskt vis få lägga ut en hel del ur egen ficka också. Det är helt OK; det är trots allt det här som är min hobby, det jag gör istället för att resa utomlands eller ha hus eller bil eller familj eller sånt. Det får kosta pengar. Jag tror att det blir en jävla bra bok, helt enkelt.

Det är mest skönt att jag nu vet exakt hur mycket allt kommer att kosta, varifrån pengarna kommer att komma, etc.

 

[krank]

UPPDATERING 2021-03-22

• Sentinels of the Weave – 30 sidor till är layoutade; nu uppe i 130. Boken är på c:a 200, så det börjar närma sig. Jag tror att de klurigare kapitlen är avklarade nu. Vi får se.
• Kutulu: Mardrömmar från Amerikat – Ekonomin i princip helt löst nu.

Jag tycker om att sitta och fippla med layout, försöka fuska in text så den passar i det utrymme den behöver få plats i. En av mina favoritdelar av rollspelsmakandet, helt klart. Framför allt när det sker utan stress.

Ett av företagen som är skyldiga mig pengar upptäckte (eller kom ihåg) idag att de var skyldiga mig mer pengar än vi tidigare trott, så plötsligt finns det några extra tusingar att hämta där. Just nu är uträkningen att om jag lägger min skatteåterbäring och alla mina nuvarande skulder från olika spelföretag på den här modulen så kommer jag bara att behöva lägga ut typ en femhundring kanske direkt ur fickan så att säga. Så nu blir det inte bara en jävla bra bok som dessutom är jävligt snygg; det blir dessutom ett färdigt och betalat projekt utan att det blir speciellt ekonomiskt jobbigt för mig. Yay!

Så nu får jag mer pengar över till att köpa… öh, andra illustrationer. Och plastgubbar, antar jag.

 

[krank]

UPPDATERING 2021-04-05

• Sentinels of the Weave – Jag fick nyss ihop en grovlayout av exempeläventyret, vilket gör att jag bara har appendix kvar.
• Kutulu: Mardrömmar från Amerikat – Alla illustrationer är klara utom typ en, och vi har som ni kanske sett ett omslag.
• More than Human 2.0 – Något slags ryck gjorde att jag började tänka på superhjältar igen. Resultatet blev den här tråden.
• Rotsystem: Alla kungens hästar, alla kungens män – Jag har suttit en stund idag och blockat ut en isometrisk karta, och försökt komma in i mina gamla tekniker och så. Det går… framåt, åtminstone.